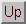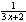
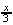 - 2
- 2
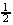 x + 3
x + 3
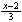


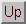


Properties of Functions
A function ƒ is defined as a set of all ordered pairs (x, y), such that for each element x, there corresponds exactly one element y.
The domain of ƒ is the set x.
The range of ƒ is the set y.
Combinations of Functions
If ƒ(x) = 3x + 1 and g(x) = x2 - 1
a) the sum ƒ(x) + g(x) = (3x + 1) + (x2 - 1) = x2 + 3x
b) the difference ƒ(x) - g(x) = (3x + 1) - (x2 - 1) = -x2 + 3x + 2
c) the product ƒ(x)g(x) = (3x + 1)(x2 - 1) = 3x3 + x2 - 3x - 1
d) the quotient ƒ(x)/g(x) = (3x + 1)/(x2 - 1)
e) the composite (ƒ ° g)(x) = ƒ(g(x))
= 3(x2 - 1) + 1 = 3x2
- 2
Inverse Functions
Functions ƒ and g are inverses of each other if
ƒ(g(x)) = x for each x in the domain of g
g(ƒ(x)) = x for each x in the domain of ƒ
The inverse of the function ƒ is denoted ƒ-1.
To find ƒ-1, switch x and y
in the original equation and solve the equation for y in
terms of x.
| Exercise: | If ƒ(x) = 3x + 2, then ƒ-1(x) = |
(A) 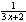
| |
(B) 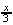 - 2 - 2
| |
| (C) 3x - 2 | |
(D) 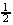 x + 3 x + 3
| |
(E) 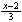
| |
| The answer is E. | x = 3y + 2 |
| 3y = x - 2 | |
y = 
|
Even and Odd Functions
The function y = ƒ(x) is even if ƒ(-x) = ƒ(x).
Even functions are symmetric about the y-axis (e.g. y = x2)
The function y = ƒ(x) is odd if ƒ(-x) = -ƒ(x).
Odd functions are symmetric about the origin (e.g. y =
x3)
| Exercise: | If the graph of y = 3x + 1 is reflected about the y-axis, |
| then an equation of the reflection is y = | |
| (A) 3x - 1 | |
| (B) log3 (x - 1) | |
| (C) log3 (x + 1) | |
| (D) 3-x + 1 | |
| (E) 1 - 3x | |
| The answer is D. | The reflection of y = ƒ(x) in the y-axis is y = ƒ(-x) |
Periodic Functions
You should be familiar with the definitions and graphs of these trigonometric functions:
sine, cosine, tangent, cotangent, secant, and cosecant
| Exercise: | If ƒ(x) = sin(tan-1 x), what is the range of ƒ? |
(A) (-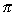 /2, /2,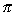 /2) /2)
| |
(B) [-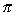 /2, /2,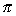 /2] /2]
| |
| (C) (0, 1] | |
| (D) (-1, 1) | |
| (E) [-1, 1] | |
| The answer is D. | The range of sin x is (E), but the points at which sin x = 1 (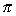 /2 + k /2 + k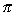 ), ),
|
| tan-1 x is undefined. Therefore, the endpoints are not included. |
Note: The range is expressed using interval notation:
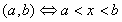
Zeros of a Function
These occur where the function ƒ(x) crosses the x-axis. These points are also called the
roots of a function.
| Exercise: | The zeros of ƒ(x) = x3 - 2x2 + x is |
| (A) 0, -1 | |
| (B) 0, 1 | |
| (C) -1 | |
| (D) 1 | |
| (E) -1, 1 | |
| The answer is B. | ƒ(x) = x(x2 - 2x + 1) = x(x -1)2 |
Properties of Graphs
You should review the following topics:
a) Intercepts
b) Symmetry
c) Asymptotes
d) Relationships between the graph of
| y = ƒ(x) and | y = kƒ(x) |
| y = ƒ(kx) | |
| y - k = ƒ(x - h) | |
| y = |ƒ(x)| | |
| y = ƒ(|x|) |