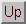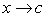 , then the following properties are true.
, then the following properties are true.

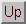


Properties of Limits
If b and c are real numbers, n is a positive
integer, and the functions ƒ and g have limits as
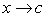
| 1. Scalar multiple: | 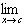 [b(ƒ(x))] = b[ [b(ƒ(x))] = b[ ƒ(x)] ƒ(x)]
|
| 2. Sum or difference: | 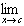 [ƒ(x) [ƒ(x)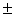 g(x)] = g(x)] = 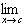 ƒ(x) ƒ(x)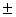 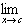 g(x) g(x)
|
| 3. Product: | 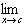 [ƒ(x)g(x)] = [ [ƒ(x)g(x)] = [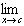 ƒ(x)][ ƒ(x)][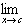 g(x)] g(x)]
|
| 4. Quotient: | 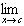 [ƒ(x)/g(x)] = [ [ƒ(x)/g(x)] = [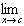 ƒ(x)]/[ ƒ(x)]/[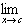 g(x)], if g(x)], if  g(x) g(x) 0 0
|
One-Sided Limits
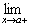 ƒ(x) ƒ(x)
| x approaches c from the right |
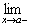 ƒ(x) ƒ(x)
| x approaches c from the left |
Limits at Infinity
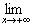 ƒ(x) = L ƒ(x) = L | 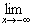 ƒ(x) = L ƒ(x) = L |
The value of ƒ(x) approaches L as x increases/decreases without bound.
y = L is
the horizontal asymptote of the graph of ƒ.
Some Nonexistent Limits
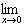 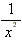
| 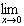 
| 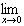 sin sin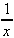
|
Some Infinite Limits
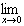 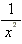 
| 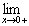 ln x ln x 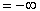
|
| Exercise: | What is 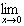 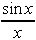 ? ?
|
| (A) 1 | |
| (B) 0 | |
(C) 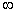
| |
(D) 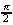
| |
| (E) The limit does not exist. /TD> | |
| The answer is A. | You should memorize this limit. |
Continuity
Definition
A function ƒ is continuous at c if:
1. ƒ(c) is defined
2. 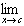
3. 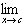
Graphically, the function is continuous at c if a pencil
can be moved along the graph of ƒ(x) through (c,
ƒ(c)) without lifting it off the graph.
| Exercise: | If 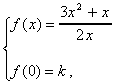 for x for x  0 0
|
| and if ƒ is continuous at x = 0, then k = | |
| (A) -3/2 | |
| (B) -1 | |
| (C) 0 | |
| (D) 1 | |
| (E) 3/2 | |
| The answer is E. | 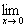 ƒ(x) = 3/2 ƒ(x) = 3/2
|
Intermediate Value Theorem
If ƒ is continuous on [a, b] and k is
any number between ƒ(a) and ƒ(b), then
there is at least one number c between a and b
such that ƒ(c) = k.